Quantum Error Correction: Google Takes on Qubit Accuracy
shutterstock: mopic
The more we hear and read about quantum computing, the more we develop a dawning comprehension for what it seems to be - along with appreciation for why it's so hard to understand. A major reason for this, as we wrote last month, is that, it's based on quantum mechanics, which has no relation to the physical laws of the "Newtonian" world we perceive around us. Quantum is based in the atomic and sub-atomic realm, where actions and reactions happen according to laws different from, and intuitively unrelated to, our level of existence. In this article, originally published in sister publication HPCwire, a Google quantum expert discusses the special qualities of the qubit, the equivalent of the bit in classical computing. We hope you'll find it educational in your ongoing quantum journey.
Quantum error correction, essential for achieving universal fault-tolerant quantum computation, is one of the main challenges of the quantum computing field and it’s top of mind for Google’s John Martinis. Delivering a presentation last week at the HPC User Forum in Tucson, Martinis, one of the world’s foremost experts in quantum computing, emphasized that building a useful quantum device is not just about the number of qubits; getting to 50 or 1,000 or 1,000,000 qubits doesn’t mean anything without quality error-corrected qubits to start with.
Martinis compares focusing on merely the number of qubits to wanting to buy a high-performance computer and only specifying the number of cores. How to create quality qubits is something that the leaders in the quantum space at this nascent stage are still figuring out. Google — as well as IBM, Intel, Rigetti, and Yale – are advancing the superconducting qubit approach to quantum computing. Microsoft, Delft, and UC Santa Barbara are involved in topological quantum computing. Photonic quantum computing and trapped ions are other approaches.
The reason quality is difficult in the first place is that qubits – the processing unit of the quantum system – are fundamentally sensitive to small errors, much more so than the classical bit. Martinis explains with a coin on the table analogy:
“If you want to think about classical bits – you can think of that as a coin on a table; we can represent classical information as heads or tails. Classical information is inherently stable. You have this coin on the table, there’s a restoring force, there’s dissipation so even if there’s a little bit of noise it’s going to be stable at zero or one. In a quantum computer you can represent [a quantum bit] not as a coin on a table but a coin in free space, where say zero is up, and one is down and rotated 90 degrees is zero plus one; and in fact you can have any amount of zero and one and it can rotate in this way to change something called quantum phase. You see since it’s kind of an analog system, it can point in any direction. This means that any small change in this is going to give you an error.
“Error correction in quantum systems is a little bit similar to what you see in classical systems where you have clocked logic so you have a memory source, where you have a clock and every clock period you can compute through some arithmetic logic and then you sequence through this and the clock timing kind of takes care of all the different delays you have in the logic. Similar here, you have kind of repetition of the error correction, based on taking the qubit and encoding it in many other qubits and doing parity measurements to see if you’re having both bit-flip errors going like this or phase flip errors going like that.”
The important thing to remember says Martinis is that if you want to have small errors, exponentially small errors, of 10-9 or 10-12, you need a lot of qubits, i.e., quantity, and pretty low error rates of about one error in one-thousand operations, i.e., quality.
In Martinis’s view, quantum computing is “a two-dimensional horse race,” where the tension between quality and quantity means you can’t think in terms of either/or; you have to think about doing both of them at the same time. Progress of the field can thus be charted on a two-dimensional plot.
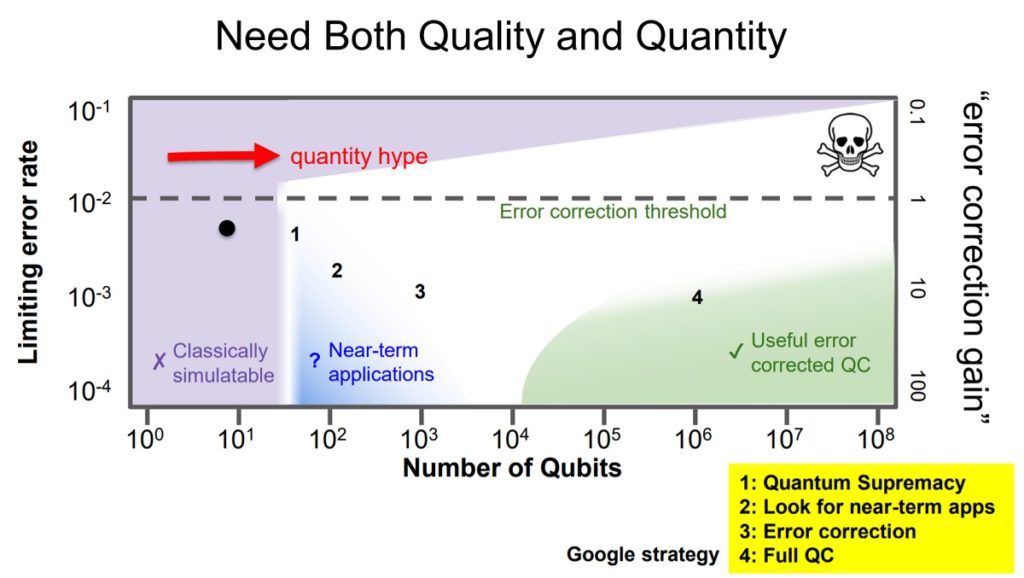The first thing to note when assessing the progress in the field are the limiting error rate and the number of qubits for a single device, says Martinis. The chart depicts, for a single device, the worst error rate, the limiting error rate, and the number of qubits. Google is aiming for an error correction of 10-3 in about 103 qubits.
“What happens, “says Martinis, “is as that error rate goes up the number of qubits you have to have to do error correction properly goes up and blows up at the error correction threshold of about 1 percent. I call this the error correction gain. It’s like building transistors with gain; if you want to make something useful you have to have an error correction that’s low enough. If the error correction is not good enough, it doesn’t matter if you have a billion qubits, you are never going to be able to make them more accurate.”
Up to 50 qubits is classically simulatable, but if the error rate is high it gets easier but it is not useful. Pointing to the lower half of the chart, Martinis says “we want to be down here and making lots of qubits. It’s only once you get down here [below the threshold] that talking quantity by itself makes sense.”
One of the challenges of staying under that error correction threshold is that scaling qubits itself can impede error correction, due to undesired cross-talk between qubits. Martinis says that the UC Santa Barbara technology it is working with was designed to reduce cross-talk to produce a scalable technology. For flux cross-talk, fledgling efforts were at 30-40 percent cross-talk. “The initial UC Santa Barbara device was between 1 percent to .1 percent cross-talk and now it’s 10-5,” says Martinis, adding “we barely can measure it.”
For the rest of this article please go to https://www.hpcwire.com/2018/04/26/google-frames-quantum-race-as-two-dimensional/
